Expressing algorithm complexity: the big O notation explained
I'd like to share a topic today which was re-introduced to me by a lightningtalk of a colleague of mine. His talk was on the "big O notation". The big O notation is a tool you can use to express the order of complexity of an algorithm.
It is useful because it lets you express the order of complexity of an algorithm without taking a lot of time profiling or researching the underlying algorithm. In other words: it gives you a quick way to gain an understanding of what might be wrong (or right) with a specific algorithm.
Disclaimer
I will be simplifying a lot of mathematics in this article, the point is using the big O notation from an information science point of view. If I made blatant mathematical mistakes, please correct me in the comments or send me an e-mail using the contact form.
The notation and a first example
The Big O notation looks at problems as a given amount of steps which need to be taken to solve a problem. It describes how the amount of steps grows with the size of a problem. Adding two numbers takes less steps than adding three numbers.
The size of the numbers is not important to the big O notation, it does not deal with the complexity of adding 2134 and 89 but with the complexity of adding two numbers in general. Of course adding 120389 and 912313 takes longer than adding 4 and 5, but the amount of steps is exactly the same.
The big O notation is a very simple one, its template is: O ( 'amount of steps' ). The placeholder 'amount of steps' is the variable part. A very first example of the notation can be found below:
class Registry
{
private $properties;
function addProperty($key, $value)
{
$this->properties[$key] = $value;
}
}
Assume you would call the addProperty function. Whatever happens, there is always one step that is taken. Written in the big O notation this looks like: O(1)
Add(), a linear function
function add()
{
$args = func_get_args();
$product = 0;
while ($arg = array_shift($args)) {
$product += $arg;
}
return $product;
}
Take a look at the function defined above (in PHP), it is designed to take a (theoretically) unlimited amount of numbers and add them all together. The resources used by this function grow linear with its input. Think away any time bootstrapping the environment and you'll see that adding 4 numbers will take twice as long as adding 2 numbers. In the big O notation this is defined as follows: O (n).
The big O notation is used to describe the upper bound of the amount of steps that need to be taken by an algorithm. So if an algorithm is O (n) all we know for sure that the algorithm will take at most n steps. Lets see another example:
function isNeedleInHaystack($needle, $haystack)
{
while ($test = array_shift($haystack) {
if ($test == $needle) {
return true;
}
}
return false;
}
If the needle is found at the first position, this function would only cycle once. If the needle is at the last position in the array or not found at all, it cycles n times, n being the size of the array. As said, the Big O notation describes the upper bound. This function is also O (n).
Upping the ante
I hope the idea of the big O notation is clear to you now, it is now time to dive in a little deeper:
function containsDuplicates($strings)
{
$c = count($strings);
for ($i = 0; $i < $c; $i++) {
for ($ii = 0; $i < $c; $ii++) {
if ($i == $ii) {
continue;
} else if ($strings[$i] == $strings[$ii]) {
return true;
}
}
}
return false;
}
This function takes an array of strings and checks if there are duplicates within this. Every position of the array is checked against every position in the array. Therefore this algorithm could be described as O (n2).
Keeping the dominant term
You might wonder whether notations as O (n^2 + 10n) are valid. To be short: they aren't. The Big O notation always describes the upper bound of the most dominant term. Let me clarify this for you with another example. Take into account the following function:
function weirdCalculation($n)
{
//I be doing n^2 + 10n stuff
}
Below is a graph of the various amount of steps taken inside the function weirdCalculation for various values of n (red line). There also is a line which neglects the 10*n part and only shows the n2 part. Based on this graph only it might not make sense to call weirdCalculation O (n2):
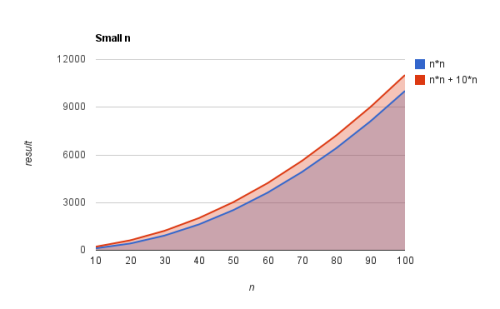
Now take a look at this second graph where larger values of n are chosen.
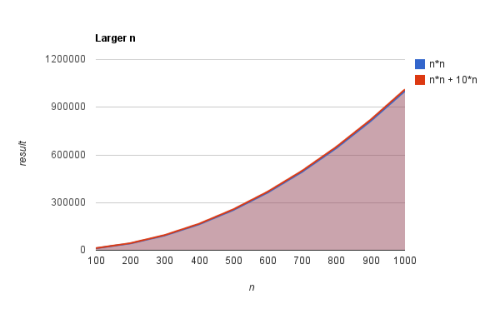
The difference is all of a sudden negligable. When you look at the first image the blue and red line move away from each other in larger steps each number. In other words, the steps that need to be taken for the red line rise faster than the steps for the blue line. If you only plotted this points in a graph you might be concerned about the 10n part and think it should matter.
If you look at the second graph however, you can see that the impact of the n2 part is much larger. The difference between the red and blue line is not really distinguishable.
O (2n)
function fib($n)
{
if ($n <= 1) {
return $n;
} else {
return fib($n - 2) + fib($n - 1);
}
}
This naive implementation of a function which calculates what number should be at position n in the fibonacci sequence starts using a lot of resources really fast. Checking with n = 40 (only resulting in 102334155) already made php use 100% cpu for 242 seconds, effectively killing it. Imagine using that on your webserver with multiple requests per second :)
Now what?
So I gave a basic introduction to the notation and offered some examples on the side. What can this do for you? Basically it should be a reminder that functions can get overly complex really quick. Solutions that seem smart (recursive function anyone), may not be that smart after all.
Whether you call it the big O notation, algorithm complexity or if you just notice three loops inside each other looping the same data, watch out! So the next time you are wondering why a function is so slow, take a quick glance and see if it is taking as little steps as possible!
Comments
-
Nice, succinct explanation - thanks very much. Another nice tutorial on Big O notation:
http://www.programmerinterview.com/index.php/data-structures/big-o-notation/
-
Take this:
<pre>
function containsDuplicates($strings)
{
$c = count($strings) - 1;
for ($i = 0; $i < $c; $i++)
{
for ($ii = $i+1; $ii <= $c; $ii++)
{
if ($strings[$i] == $strings[$ii]) return true;
}
}
return false;
}</pre>
The exact step calculation is (n*(n-1)/2) basically twice as fast as your example for the same result. It's still O(n^2), right?
Even though the graphical step count between the two is greatly divergent? -
Nice, put in HTML tags and code keeps format in preview and then escaped when shown, wiping out the line feeds.
Stranger still, pumping in extra line feeds before and after one line. -
Can you explain the Fibonacci example. I took the value of n=3, and could only count 5 operations... How exactly did we come up with O(2^n) for that example?
 After about 10 years of professional development at both
After about 10 years of professional development at both